The monkeys that beat the market
The craziest investment strategy that actually worked
“A blindfolded monkey throwing darts at a newspaper’s financial pages could select a portfolio that would do just as well as one carefully selected by experts.”
Burton Malkiel wrote this in 1973, in his book “A Random Walk on Wall Street” and it stirred up a lot of controversy. Of course! The entire basis for active fund management was under attack, and a statement like this made them look not just incompetent, but comically absurd as well.

What took the cake was the fact that someone actually tested out Malkiel and showed that he might be right! In an experiment tracked by the Wall Street Journal, a monkey picked a limited number of stocks that consistently beat the market. Famous TV presenter John Stossel did his own version of the experiment taking the monkey's place and reported higher returns as well.
Monkeys were not the only animals that proved to be genius traders.
In 2012, a cat named Orlando made headlines for beating a team of investors narrowly over the span of a year. It made its “trading decisions” by dropping a toy mouse on a grid of numbers allocated to different companies. The result? The cat turned £5,000 into £5,542 while the investment professionals made £5,176!
Another absurd case was that of Michael Marcovici, an Austrian concept artist breeding and training “rat traders” with names like Morgan Kleinsworth and Mr. Lehmann whom he claimed had a 57% accuracy rate!
Crazy, right? But there's an unspoken truth here: The vast majority of animal prophets who pick stocks would not make the news, because they fail. Even a broken clock is correct twice a day, so is there more to this than just entertaining anecdotes? Can the “monkey index fund” stand the test of an experiment?
That's exactly what Robert Arnott and his team at Research Affiliates LLC set out to find.
The great monkey experiment
The idea was simple: Instead of actually managing a monkey, the team simulated a monkey’s picks by randomly selecting 30 stocks from the top 1000 stocks by market capitalization and making an equally weighted index from it. The same process was repeated 100 times and the average returns were compared from 1964 to 2012.
Burton Malkiel had said that a monkey would do as well as mutual funds. He was wrong. The monkey actually beat the market 96 times out of 100!
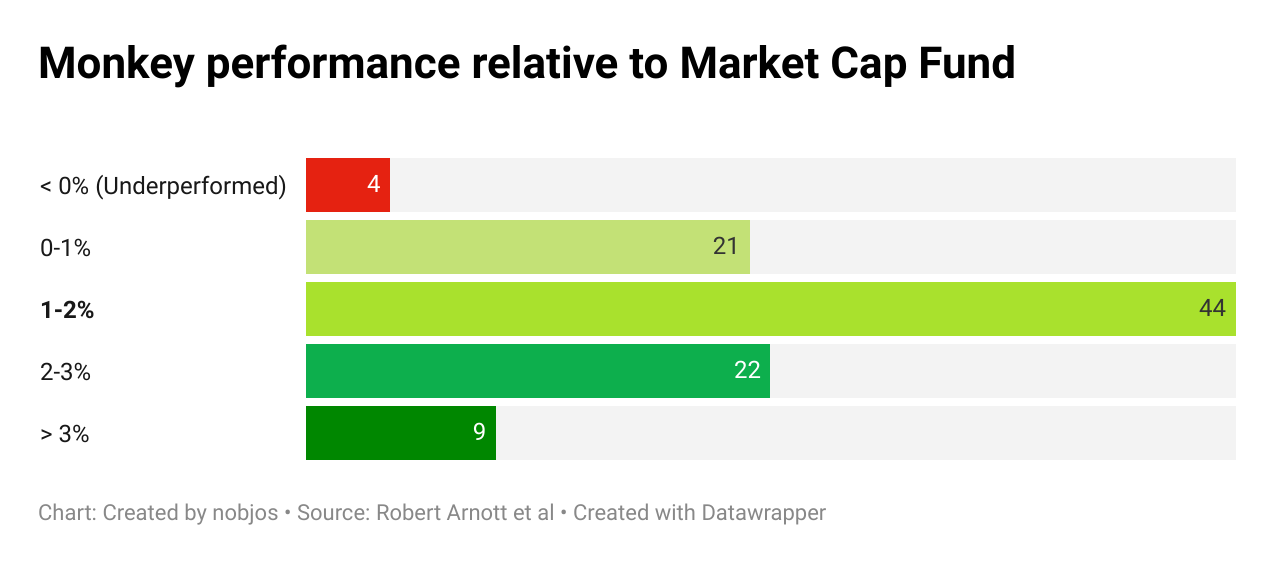
The graph above shows the distribution of the returns. In 75% of the cases, the monkey beat the market cap benchmark by more than 1%, and 30% of the time, it got a relative profit of greater than 2%! The returns of the monkey index fund were not only higher, but they were also better in terms of risk-adjusted return based on the Sharpe ratio. In terms of standard deviation though, the risk was slightly higher.
Round 2
This was not the only experiment. Researchers from Cass university leveraged Rob Arnott's experiment to design their own: They picked stocks from a pool of 1000 without the restriction of equal weighting and compared the returns against the market - They did this for 10 million different portfolios for each year between 1968 and 2011. The results were mindblowing:
An investment of $100 in the US market in 1968 would have made just under $5000 by the end of 2011.
Half the monkeys generated more than $8,700.
A quarter returned more than $9,100.
10 percent made more than $9,500 - A 940% profit or more!
But the study went further. The 3-year rolling average of the monkeys’ performance was taken and compared against the market cap fund year by year from 1972-2012 to check: What proportion of monkeys beat the market every year? These were the results:
These numbers show how all-or-nothing the whole venture is. All the monkeys beat the market about 57% of the time, but they all underperformed the market about 31% of the time. The timing is also revealing: The monkeys win during bull runs but underperform for long stretches during bear markets. This is where the psychological element comes into play. It’s all fun and games when the going is good, but would you have the confidence to perform worse than the market for 5 to 6 years in a row betting on a monkey’s predictions?
Having said that, it’s still no joke that the monkeys beat the market cap funds about 60% of the time. The figures from earlier reveal that the average performance over the entire period is also better than market cap funds.
So how did they do it? Were the monkeys stock-picking geniuses?
Indexing is the key
Before you run to the pet store looking for a dart-throwing monkey, let's try to figure out why this works in the first place. The reason for the monkeys’ success is hidden in where they came up short. If you look again at the data collected by the Rob Arnott team, you can see two things:
Volatility (beta) is more in the case of the monkey index fund
Equally weighted market index funds beat even the monkey index funds
How market index funds are created might play an even bigger role than the individual stocks that are picked for the fund. In market cap based index funds like the S&P500, the weightage given to the companies isn't equal - It's based on their market capitalization. In times of turmoil, these funds are supposed to give more stability to the portfolio because they don't fluctuate as much. But that also means that your scope for growth is limited because there's only so much that big companies can grow.
In an equally-weighted index fund, on the other hand, the returns from the growth of small and value stocks are captured as well, but the price you pay is (supposedly) higher volatility. In the case of the monkeys picking random stocks, this is what happened - Equal exposure to a few small stocks that saw massive growth balanced out the losses from other stocks. It seemed like a gamble though, because of the risk involved.
From 2000 onwards, equally-weighted index funds have outperformed SPY by more than 100%. The catch is that though Sharpe ratio looks similar, the volatility was more in the case of equally-weighted funds as shown by the standard deviation, with higher drawdowns as well during times of crashes. The higher returns provided by these stocks were a trade-off for the exposure to this volatility.
Conclusion
If one puts an infinite number of monkeys in front of (strongly built) typewriters and lets them clap away (without destroying the machinery), there is a certainty that one of them will come out with an exact version of the 'Iliad.' Once that hero among monkeys is found, would any reader invest their life's savings on a bet that the monkey would write the 'Odyssey' next?
- Nicholas Nassim Taleb
The problem with fascinating strategies is that they might not be repeatable.
The extraordinary performance of randomly picked stocks does not mean that any pick you make will work. It just means that where there are outsized rewards, there are outsized risks as well. Most unknown stocks that make the headlines for exponential growth fall into the category of either small stocks or value stocks, and if you invest in them, you are rewarded for the risk you are taking on. Market beta, Value, and Size - Exposure to these three decide the nature of your portfolio.
What you should take away from this article is that your exposure to these three factors need not be constant! A market cap based Index fund might not be the only solution for safe investing. There are other possibilities out there with a slightly different risk-reward ratio.
It might be worth it to take a look at what the alternatives are.
See you next time with another quick read!
This is a quick read. I write more in-depth articles like my strategy for consistent returns from the crypto market and investing strategies for every risk level on my weekly newsletter Market Sentiment. You can subscribe here:
Disclaimer: I am not a financial advisor. Do not consider this as financial advice.
If you enjoyed this piece, please do us the HUGE favor of simply liking and sharing it with one other person who you think would enjoy this article! Thank you.






Always interesting, well researched and useful information. I'm so glad I signed up for your blog. Thanks again for your hard work!
I just saw a video of michael reeves that made a fish pick stocks and compared it to listening to wall street bets. I think that the fish also outperformed the market.
https://www.youtube.com/watch?v=USKD3vPD6ZA