The Devil's Card Game
Don't risk what you have and need for what you don't have and don't need.
We are publishing this without a paywall.
At a fundamental level, investing is just one form of making a bet. It’s essential, however, that the bet be made in a way that is investing (net present value positive) rather than gambling (net present value negative). — Bill Gross, Co-founder PIMCO
Since you obviously are here for the game, let’s jump right in:
There are 11 cards face down on a table. 10 are double cards, and 1 is the devil card. You start with $1 million, and then you have to choose the cards one by one (without replacement). As the name suggests, you double your money if you pick a double card. But, if you pick the devil card, your money gets divided by 2048 (i.e., you lose 99.95%).
You are free to stop picking cards anytime and walk away with whatever money you have at that point. How will you play this game? And when will you walk away?
While this looks like a simple card game, thinking through this can teach us important concepts about investing.
The game is an exaggerated version of what happens in the market. Instead of cards, we pick stocks. While our investments do not double instantaneously, most generate decent returns. However, there is a slight chance the company we invest in goes bankrupt or the market enters a recession at the same time we do lump sum investing.
Just like in the card game, deciding how much risk to take and when to get out is instrumental in maximizing our returns. The same strategy we use to optimize the Devil’s Card Game returns can also help us invest better.
The best and worst scenarios
The game is about balancing the risk of picking the devil card against the potential reward of doubling our money. To know when to walk away, we must first find the best and worst-case scenarios we can encounter while playing the game.
In the best-case scenario, we draw all ten double cards without drawing the devil card. We can stop at the 10th draw since we know for certain that the 11th card is the devil card. Since we start with a million, our total payout would be a cool $1.02 billion.
On the other hand, the worst-case scenario is drawing the devil card in one of the draws. Irrespective of when we pick it, once we have picked it, it makes logical sense to pick all the other cards (since we know that all of them are double cards now). That leaves us with $500K.
Assuming the game won’t allow us to cash out without drawing a card, the expected payout from the game is between $500K and $1 Billion.
How many cards to pick?
Calculating the expected value for each number of card draws is a simple way to determine the optimum number of cards to pick.
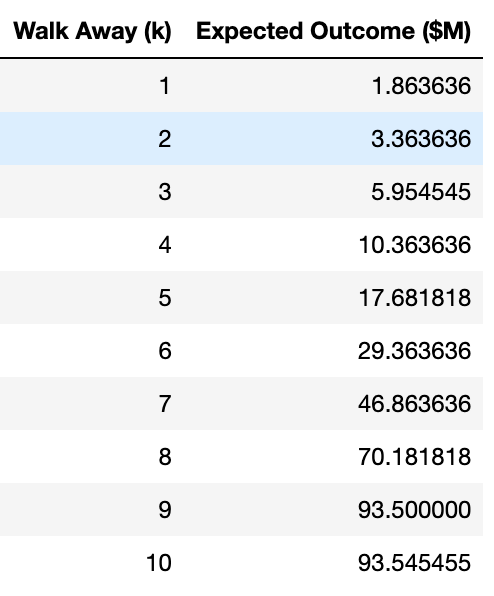
If you pick just one card, there is a 1/11 chance of drawing the devil card and a 10/11 chance of doubling the money. So, the expected value would be $1.8 million.
We can extrapolate this and run all the scenarios in the game as a simulation to get the expected outcome for all scenarios1.
If we solely base our picks on the expected value, we must draw all 10 cards. But, as we highlighted here, the problem with finding the average expected outcome is that your outcome might be very different from the average outcome. You can only play the game once — just because the average is good doesn’t imply a great outcome for you.
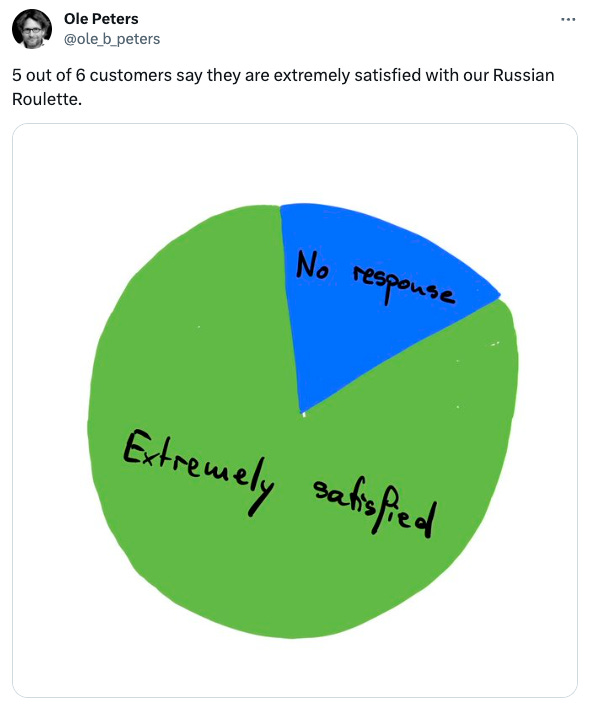
As Dr. Ole Peters puts it, it would be akin to taking the customer survey for a game of Russian Roulette and concluding it’s a great game.
To put this into perspective, consider your situation after 9 successful draws:
You are sitting with $512M, and the last draw is now a 50/50 bet on whether you will double your money or lose 99.95% of it. Most of us would not take the last draw and leave with $512M. Realistically, everything you want to do with a billion, you can do with half a billion.
That brings us to the
Marginal Utility of Money
The best way to understand the marginal utility is by playing the below game.
The “right” answer here is getting the coin toss — Because your expected value is $500K by taking the toss. But realistically, even $100K is a life-changing sum for most of us, and we would take that guaranteed amount over a 50/50 chance of getting the million.
Now, if we change the amount to $100 instead of $1 million, a higher proportion of us will choose the coin toss as we prefer the 50/50 chance of getting $100 over the guaranteed $10 payout, as $10 can’t make any significant difference to our lives.
Finally, if we ask a billionaire like Bezos or Musk to play the same game, they will almost always choose the coin toss as an added $100K will barely make any difference to them.
This is why calculating the expected outcome is irrelevant in real-life scenarios. Instead, we should calculate the expected utility of winning based on our current net worth.
Assuming the person who is playing has a net worth of $1M, the expected utility after 1 draw will be (assuming the utility function is logarithmic — like shown above)
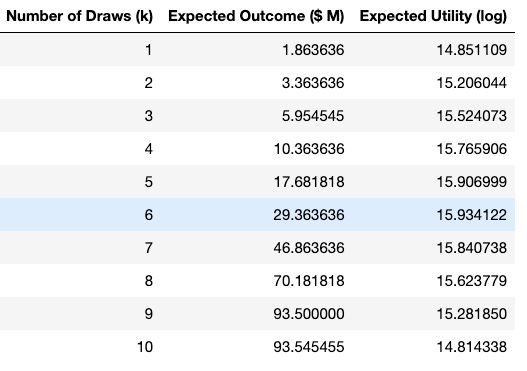
Simulating this for all draws2, we see that even though the expected outcome is higher for more draws, the expected utility of the winnings decreases after the fifth draw. So, someone with a $1M net worth should optimally stop after drawing six times.
(For those who are curious, if your starting net worth is $10M, you should draw 7 times, and if your net worth is $100M, you should draw 8 times).
This game illustrates perfectly the absurdity of taking unnecessary risks in the market.
Assume you have a $100K portfolio, and the market is chugging along fine, giving a 10% return. After getting “inspired” by Wallstreetbets, you try to double the index returns by investing in sketchy stocks and risky plays. Even if you come out on the other side with a 20% return, what is the marginal utility of the added $10K you gained? Was it worth the risk of blowing up your portfolio?
To close, we will leave you with Warren Buffett’s notes from Berkshire’s 2018 annual letter.
We use debt sparingly. Many managers, it should be noted, will disagree with this policy, arguing that significant debt juices the returns for equity owners. And these more venturesome CEOs will be right most of the time.
At rare and unpredictable intervals, however, credit vanishes and debt becomes financially fatal. A Russian-roulette equation - usually win, occasionally die - may make financial sense for someone who gets a piece of a company's upside but does not share in its downside. But that strategy would be madness for Berkshire.
Rational people don't risk what they have and need for what they don't have and don't need.
If you enjoyed this, you will find this interesting:
One of the most overlooked aspects of investing is Shannon's Demon: Using it, we can consistently generate positive returns from two uncorrelated assets having zero expected long-term returns. P.S. — This post was inspired by this incredible 40-tweet thread by 10-K Diver. It’s a must-read and goes deeper into concepts of partial betting, Kelly Criterion, and much more. He has also highlighted a truly brilliant concept called Backwards Induction, by which we can guarantee a take-home of ~$170.86M — Even if you draw the devil as your first card.
Footnotes
## Expected outcome simulation code
def calculate_expected_outcomes():
initial_money = 1000000
num_cards = 11
devil_penalty = 2048
outcomes = []
for k in range(1, 11):
outcome_1 = (2**k) * initial_money / 1000000
prob_1 = 1 - (k / num_cards)
outcome_2 = 500000 / 1000000
prob_2 = k / num_cards
expected_outcome = (outcome_1 * prob_1) + (outcome_2 * prob_2)
outcomes.append((k, expected_outcome))
return outcomes
expected_outcomes = calculate_expected_outcomes()
df = pd.DataFrame(expected_outcomes, columns=["Walk Away (k)", "Expected Outcome ($M)"])## Marginal utility simulation code
import numpy as np
import pandas as pd
def calculate_expected_outcomes_with_utility():
num_cards = 11
net_worth = 1000000
initial_money = 1000000
devil_penalty = 2048
expected_outcomes = []
for k in range(1, 11):
outcome_1 = (2**k) * initial_money
prob_1 = 1 - (k / num_cards)
outcome_2 = 500000
prob_2 = k / num_cards
expected_outcome = ((outcome_1 * prob_1) + (outcome_2 * prob_2))/1000000
total_money_double = net_worth + outcome_1
total_money_devil = net_worth + outcome_2
expected_utility = (prob_1 * np.log(total_money_double)) + (prob_2 * np.log(total_money_devil))
expected_outcomes.append((k, expected_outcome, expected_utility))
return expected_outcomes
expected_outcomes_with_utility = calculate_expected_outcomes_with_utility()
# Convert to DataFrame for better display
df = pd.DataFrame(expected_outcomes_with_utility, columns=["Number of Draws (k)", "Expected Outcome ($ M)", "Expected Utility (log)"])
print(df)